Games101:变换 & 光栅化
Overview总览
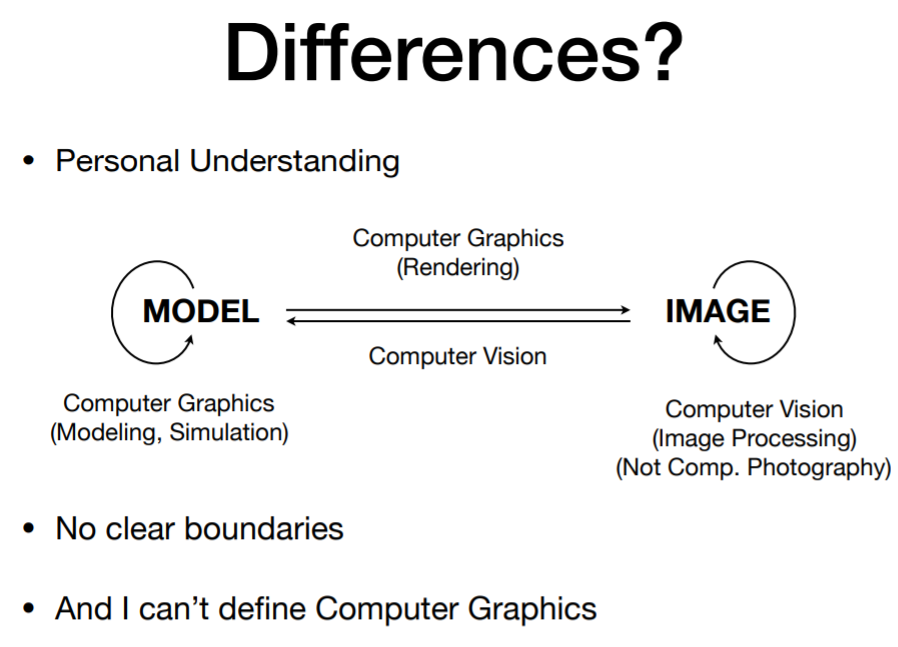
图形学与计算机视觉的区别
图形学研究的是把模型渲染为图片,计算机视觉是分析图片重建出模型
Linear Algebra线性代数回顾
向量运算
\[ \overrightarrow{a}\ \cdot \ \overrightarrow{b}= \begin{pmatrix} x_a\\y_a\\z_a \end{pmatrix} \cdot \begin{pmatrix} x_b\\y_b\\z_b \end{pmatrix} =x_ax_b+y_ay_b+z_az_b \]
\[ \overrightarrow{a}\ \times\ \overrightarrow{b}=A*b= \begin{pmatrix} 0 & -z_a & y_a\\ z_a & 0 & -x_a\\ -y_a & x_a & 0 \end{pmatrix} \begin{pmatrix} x_b\\y_b\\z_b \end{pmatrix}= \begin{pmatrix} y_az_b - y_bz_a\\ z_ax_b - x_az_b\\ x_ay_b - y_ax_b \end{pmatrix} \]
点乘可用于计算夹角、分解向量
叉乘可以得到右手系、判断左右关系、点与封闭图形的内外关系
矩阵运算
矩阵乘法:前行乘后列
逆:相乘为单位阵
Transformation变换
变换矩阵
齐次坐标系添加的一维
表示点的位置时最后一个数为1,而表示方向时最后一个数为0。
- 表示方向的向量可以平移,左乘位移矩阵之后不变。
- \(vector+vector=vector\)
- \(point-point=vector\)
- \(point+vector=point\)
- \(point+point=两point中点\)
表示位置时,只要最后一个数字w非0,表示的都是统一除以w之后的那个点
仿射变换
线性变换指的是保留了矢量加和标量乘的性质:\(f(x)+f(y)=f(x+y)\)、\(kf(x)=f(kx)\)
线性变换(缩放和旋转)+平移。可以多种复杂变换进行组合,表达的是先进行线性变换然后平移。得到的结果仍然是一个矩阵,存储的数据量没变,而且最后一行一定是\((0,0,0,1)\)
Scale \[ \begin{pmatrix} s_x & 0 & 0 & 0\\ 0 & s_y & 0 & 0\\ 0 & 0 & s_z & 0\\ 0 & 0 & 0 & 1 \end{pmatrix} \]
Rotation \[ R_x(\alpha)= \begin{pmatrix} 1 & 0 & 0 & 0\\ 0 & cos\alpha & -sin\alpha & 0\\ 0 & sin\alpha & cos\alpha & 0\\ 0 & 0 & 0 & 1 \end{pmatrix},\ R_y(\alpha)= \begin{pmatrix} cos\alpha & 0 & sin\alpha & 0\\ 0 & 1 & 0 & 0\\ -sin\alpha & 0 & cos\alpha & 0\\ 0 & 0 & 0 & 1 \end{pmatrix},\ R_z(\alpha)= \begin{pmatrix} cos\alpha & -sin\alpha & 0 & 0\\ sin\alpha & cos\alpha & 0 & 0\\ 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 1 \end{pmatrix} \]
Translation \[ \begin{pmatrix} 1 & 0 & 0 & t_x\\ 0 & 1 & 0 & t_y\\ 0 & 0 & 1 & t_z\\ 0 & 0 & 0 & 1 \end{pmatrix} \]
依次经过“缩放-旋转-平移”,也就是\(M_{Trans}*(M_{RotZ}*M_{RotY}*M_{RotX})*M_{Scale}\)对应的矩阵为:
\[ \begin{pmatrix} S_x * cosR_y*cosR_z & S_y * (sinR_x*sinR_y*cosR_z - cosR_x*sinR_z) & S_z * (cosRx*sinRy*cosRz + sinRx*sinR_z) & T_x\\ S_x * cosR_y*sinR_z & S_y * (sinR_x*sinR_y*sinR_z + cosR_x*cosR_z) & S_z * (cosRx*sinRy*sinRz - sinRx*cosRz) & T_y\\ -S_x * sinR_y & S_y * sinR_x*cosR_y & S_z * cosR_x*cosR_y & T_z\\ 0 & 0 & 0 & 1 \end{pmatrix} \]
在数学运算上:列向量 => 变换矩阵要左乘 => 乘法右结合 => 各分量矩阵需要逐个左乘得到组合变换矩阵
在其它的框架里,因为可能使用的是行向量或者列优先存储的矩阵,所以可能会有些不一样
旋转矩阵结构
绕一个轴旋转时,对应的坐标不会发生变换,对应就是十字线中心为1,其它为0
绕Y轴旋转的矩阵有些特殊,是因为\(x\times y=z\)、\(y \times z = z\),而\(z \times x = y\)
欧拉角
\(R_{xyz}(\alpha,\beta,\gamma)=R_x(\alpha)R_y(\beta)R_z(\gamma)\)
如果是绕任意轴进行旋转,当轴不过原点时,就先移到原点,旋转之后再移回去
旋转结果不仅却决于xyz轴顺序,还取决于是本地坐标系还是世界坐标系
四元数的作用
方便进行旋转角度插值
View Transformation观测变换
确定相机位置
需要位置\(e\)、前\(g\)、上\(t\)(防止发生roll)
把相机变换到标准位置
标准位置是指:位置处于(0, 0, 0),看向-z,上为y轴。
因为之后需要进行投影,只要保持相机和物体相对位置不变,得到的结果就不会改变。于是可以把相机和物体整体进行变换。
为了之后的方便以及约定俗成,规定把相机变换到标准位置,这个过程需要用到一个变换矩阵,那么物体也需要进行相同的变换,也需要乘以相同的变换矩阵。这个过程就叫做观测变换。
求观测变换矩阵
首先使用\(T_{view}\)把相机平移到坐标原点,然后旋转以对齐三个轴。平移很容易求,但是旋转不好求。改为先计算逆变换的矩阵,也就是把世界坐标轴变换到与相机的三个轴相重合(X轴转到右边(\(g\times t\)),Y轴转到上边(\(t\)),Z轴转到后边(\(-g\)))。
这个矩阵很好理解,与每个轴相乘就是需要的结果 \[ \begin{pmatrix} (g\times t).x & (t).x & (-g).x & 0\\ (g\times t).y & (t).y & (-g).y & 0\\ (g\times t).z & (t).z & (-g).z & 0\\ 0& 0 & 0 & 1 \end{pmatrix} \]
根据旋转矩阵的正定性(每行为相互垂直的单位向量的矩阵是正定的),转置矩阵就是其逆矩阵,从而可以快速得到对应的变换矩阵\(R_{view}\)。
从而整个观测变换矩阵就是 \[ \begin{aligned} M_{view} = R_{view}*T_{view} &= \begin{pmatrix} 1 & 0 & 0 & -e.x \\ 0 & 1 & 0 & -e.y \\ 0 & 0 & 1 & -e.z \\ 0 & 0 & 0 & 1 \end{pmatrix} \begin{pmatrix} (g\times t).x & (g\times t).y & (g\times t).z & 0\\ (t).x & (t).y & (t).z & 0\\ (-g).x & (-g).y & (-g).z & 0\\ 0 & 0 & 0 & 1 \end{pmatrix}\\\\ &= \begin{pmatrix} (g\times t).x & (g\times t).y & (g\times t).z & -e.x\\ (t).x & (t).y & (t).z & -e.y\\ (-g).x & (-g).y & (-g).z & -e.z\\ 0 & 0 & 0 & 1 \end{pmatrix} \end{aligned} \]
值得注意的是,这个矩阵左上角3x3的三行分别对应着相机的X、Y、Z轴在世界坐标系中的表示,矩阵的最后一列与相机的世界坐标恰好相反
Project Transformation投影变换
Orthographic Projection正交投影
平截头体的边界
左\(l\)、右\(r\)、上\(t\)、下\(b\)、近\(n\)、远\(f\)
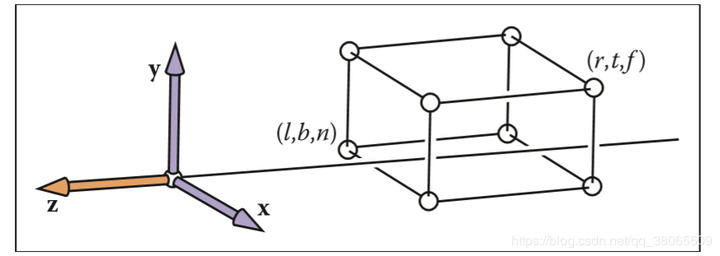
正交投影过程
先将平截头体的中心移动到原点(相机位置),然后缩放为\([-1,1]^3\)的标准立方体(为了之后的方便、约定俗成)。所用矩阵为:
$$ \[\begin{aligned} M_{ortho} &= \begin{pmatrix} \frac{2}{r-l} & 0 & 0 & 0\\ 0 & \frac{2}{t-b} & 0 & 0\\ 0 & 0 & \frac{2}{n-f} & 0\\ 0 & 0 & 0 & 1\\ \end{pmatrix} \begin{pmatrix} 1 & 0 & 0 & -\frac{r+l}{2}\\ 0 & 1 & 0 & -\frac{t+b}{2}\\ 0 & 0 & 1 & -\frac{n+f}{2}\\ 0 & 0 & 0 & 1\\ \end{pmatrix} \\\\ &= \begin{pmatrix} \frac{2}{r-l} & 0 & 0 & \frac{l+r}{l-r}\\ 0 & \frac{2}{t-b} & 0 & \frac{b+t}{b-t}\\ 0 & 0 & \frac{2}{n-f} & \frac{f+n}{f-n}\\ 0 & 0 & 0 & 1\\ \end{pmatrix} \end{aligned}\]$$
虽然这个过程会拉伸物体,但是之后还会有视口变换拉回来(这里的变换其实是为了之后的视口变换方便)
注意这里缩放矩阵三行三列的分母不是\(f-n\),因为这里是右手系,z朝屏幕外面,近平面的z更大
但这是在f和n都定义为负数的情况。实际上在OpenGL里的NDC是左手系(虽然之前MV变换都是右手系),经常定义的n和f都是到相机的距离(比如0.1和100),是正数。对应所用矩阵为:
$$ \[\begin{aligned} M_{ortho} &= \begin{pmatrix} \frac{2}{r-l} & 0 & 0 & 0\\ 0 & \frac{2}{t-b} & 0 & 0\\ 0 & 0 & \frac{2}{f-n} & 0\\ 0 & 0 & 0 & 1\\ \end{pmatrix} \begin{pmatrix} 1 & 0 & 0 & -\frac{r+l}{2}\\ 0 & 1 & 0 & -\frac{t+b}{2}\\ 0 & 0 & 1 & -\frac{n+f}{2}\\ 0 & 0 & 0 & 1\\ \end{pmatrix} \\\\ &= \begin{pmatrix} \frac{2}{r-l} & 0 & 0 & \frac{l+r}{l-r}\\ 0 & \frac{2}{t-b} & 0 & \frac{b+t}{b-t}\\ 0 & 0 & \frac{2}{f-n} & \frac{n+f}{n-f}\\ 0 & 0 & 0 & 1\\ \end{pmatrix} \end{aligned}\]$$
透视投影
近大远小(因为后面变换的时候压缩了远平面),平行线不再平行。平时画的那种立方体都是正交投影。
平截头体定义
近\(n\)、远\(f\)、fov角(上下张角)、宽高比
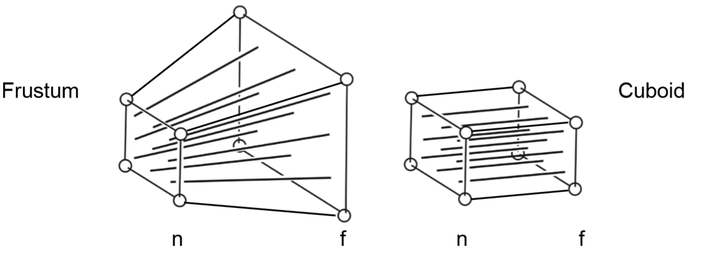
透视投影过程
挤压远平面到跟近平面一样大,然后进行正交投影。挤压过程中,点会靠近远平面。
求第一步用到的压缩矩阵,其实就是要知道一个点被变换之后的坐标。首先根据相似三角形,可以知道\(y'=\frac{n}{z}y\)、\(x'=\frac{n}{z}x\),其中z是变换之前的。对应齐次坐标就是\((\frac{n}{z}x,\frac{n}{z}y,z',1)^T\),等价于\((nx,ny,nz',n)^T\),所以这个压缩矩阵一定是 \[ \begin{pmatrix} n & 0 & 0 & 0\\ 0 & n & 0 & 0\\ ? & ? & ? & ?\\ 0 & 0 & 1 & 0 \end{pmatrix} \] 然后根据近平面上的所有点\((x,y,n,1)^T\)和远平面的中心点\((0,0,f,1)^T\)被矩阵变换之后不变,可以列出等式,最后解出这个矩阵 \[ \begin{pmatrix} n & 0 & 0 & 0\\ 0 & n & 0 & 0\\ 0 & 0 & n+f & -fn\\ 0 & 0 & 1 & 0 \end{pmatrix} \] 求出压缩矩阵,剩下就是正交投影,从而透视投影矩阵是 \[ M_{persp} = M_{ortho}* \begin{pmatrix} n & 0 & 0 & 0\\ 0 & n & 0 & 0\\ 0 & 0 & n+f & -fn\\ 0 & 0 & 1 & 0 \end{pmatrix}= \begin{pmatrix} \frac{2n}{r-l} & 0 & \frac{l+r}{l-r} & 0\\ 0 & \frac{2n}{t-b} & \frac{b+t}{b-t} & 0\\ 0 & 0 & \frac{n+f}{n-f} & \frac{2nf}{f-n}\\ 0 & 0 & 1 & 0 \end{pmatrix} \] 注意这里n和f是负数,如果是OpenGL的投影变换: \[ M_{persp} = M_{ortho}* \begin{pmatrix} n & 0 & 0 & 0\\ 0 & n & 0 & 0\\ 0 & 0 & n+f & -fn\\ 0 & 0 & 1 & 0 \end{pmatrix}= \begin{pmatrix} \frac{2n}{r-l} & 0 & \frac{l+r}{l-r} & 0\\ 0 & \frac{2n}{t-b} & \frac{b+t}{b-t} & 0\\ 0 & 0 & \frac{f+n}{f-n} & \frac{2nf}{n-f}\\ 0 & 0 & 1 & 0 \end{pmatrix} \] 因为最后用的也是正交投影,所以跟正交投影一样,最后都是变换到了\([-1,1]^3\)的标准立方体里
最后一行不是\((0,0,0,1)\),说明透视投影不是仿射变换
Rasterization光栅化
光栅化就是指绘制到屏幕上
屏幕空间
对之前的标准立方体拉伸x和y并平移中心到屏幕中心(z不变),然后离散化,与屏幕像素点做映射。最左下角的像素坐标为(0,0),但是因为像素有大小,像素中心并不是像素下标。
关于深度值z
在OpenGL里是先平移然后拉伸(屏幕宽度为\(w\)高度为\(h\)),并且对z值进行了线性映射,从[-1,1]映射到[0,1],而且由于之前投影变换到NDC之后变成了左手系,这时远平面(1)对应1,近平面(-1)对应0。 \[ M_{viewport}= \begin{pmatrix} \frac{w}{2} & 0 & 0 & \frac{w}{2}\\ 0 & \frac{h}{2} & 0 & \frac{h}{2}\\ 0 & 0 & \frac{1}{2} & \frac{1}{2}\\ 0 & 0 & 0 & 1 \end{pmatrix} \] (如果仍然保持右手系,那么n和f都是负的,对应第三行第三列应该是\(-\frac{1}{2}\)才能把远平面对应到1,近平面对应到0)
虽然在视口变换对z进行的是线性映射,但是相对于摄像机视角下的观察空间坐标(MV变换之后)来说并不一定是线性的。
如果是正交投影,z是线性变化的
$$ \[\begin{aligned} \begin{pmatrix} x_{viewport}\\y_{viewport}\\z_{viewport} \end{pmatrix} &= M_{viewport} * M_{ortho} * \begin{pmatrix} x_{view}\\y_{view}\\z_{view}\\1 \end{pmatrix} \\\\ &= \begin{pmatrix} \frac{w}{r-l} & 0 & 0 & \frac{lw}{l-r}\\ 0 & \frac{h}{t-b} & 0 & \frac{bh}{b-t}\\ 0 & 0 & \frac{l}{f-n} & \frac{n}{n-f}\\ 0 & 0 & 0 & 1 \end{pmatrix} * \begin{pmatrix} x_{view}\\y_{view}\\z_{view}\\1 \end{pmatrix} \\\\ &= \begin{pmatrix} w\frac{l-x_{view}}{l-r}\\ h\frac{b-y_{view}}{b-t} \\ \frac{z-n}{f-n} \\ 1 \end{pmatrix} \end{aligned}\]$$
如果是透视投影
$$ \[\begin{aligned} \begin{pmatrix} x_{viewport}\\y_{viewport}\\z_{viewport} \end{pmatrix} &= M_{viewport} * M_{persp} * \begin{pmatrix} x_{view}\\y_{view}\\z_{view}\\1 \end{pmatrix} \\\\ &= \begin{pmatrix} \frac{nw}{r-l} & 0 & \frac{lw}{l-r} & 0\\ 0 & \frac{hn}{t-b} & \frac{bh}{b-t} & 0\\ 0 & 0 & \frac{f}{f-n} & \frac{bf}{n-f}\\ 0 & 0 & 1 & 0 \end{pmatrix} * \begin{pmatrix} x_{view}\\y_{view}\\z_{view}\\1 \end{pmatrix} \\\\ &= \begin{pmatrix} w\frac{lz_{view}-nx_{view}}{l-r}\\ h\frac{bz_{view}-ny_{view}}{b-t} \\ f\frac{z-n}{f-n} \\ z \end{pmatrix} \end{aligned}\]$$
之后执行透视除法,统一除以w分量(这里值为z),得到\(z_{viewport}=\frac{1/z_{view}-1/n}{1/f-1/n}\),是反比例函数
所谓透视除法实际上只是一个归一化操作,并不改变点的坐标含义。比如:(3, 6, 9, 3)和(1, 2, 3, 1)在齐次坐标系中表示的是同一个点,只不过第二个是执行了透视除法之后的结果。
映射过程
基本图元是三角形,需要判断像素点是否在三角形内,因为像素有大小,实际上是判断像素点中心是否在三角形内,通过三次叉乘结果是否符号都相同进行判断。
加速
使用包围盒,提前求出一个三角形的矩形范围,或者对每一行都求出像素点坐标的范围。
反走样
还是因为像素有大小,而且像素内的颜色单一,通过像素点中心进行直接映射得到的结果会有很明显的锯齿。本质原因是采样频率不足。傅里叶分解可以拟合任意函数,比如要拟合的是正弦函数,当正弦函数频率很高而采样点不足时,拟合的效果很不好(拟合出来的是低频的)
所以可以降低原有频率或者提高采样频率。前者就是先做模糊处理(低通滤波去掉高频)再采样,后者有通过直接增加像素点个数的超采样,或者在像素点内增加采样点,而实际上每个像素点只运行一次片段着色器,只是需要给增加的采样点也准备颜色、深度、模板缓冲,MSAA。
更快的是采用图像处理技术,直接对有锯齿的图进行边缘替换,FXAA